[논문리뷰] SWA: Averaging Weights Leads to Wider Optima and Better Generalization (UAI ‘18)
대회에서 몇 번 봤었는데, 어떤 내용인지 궁금해서 읽어봤습니다.
한 줄로 요약하면, SWA는 loss surface 상에서 broader하고 flat한 optima를 찾을 수 있는 방법으로, 일반화 성능도 높일 수 있으며 일반적인 ensemble보다 효율적입니다.
0. Abstract
저자들이 제안한 Stochastic Weight Averaging (SWA)는 cyclical or constant LR로 SGD trajectory를 따라 여러 weight의 평균을 내는 방식으로 기존의 SGD보다 더 좋은 일반화 성능을 보입니다. 또한 SGD 보다 flat한 solution을 잘 찾으면서, 단 하나의 모델의 output만으로도 여러 모델의 output을 사용하는 Fast Geometric Ensembling (FGE) 방식을 근사하는 것으로 보입니다. 다양한 Dataset과 Model로 검증한 결과를 요약하면, SWA는 실행이 쉽고 높은 일반화 성능과 함께 추가 연산이 거의 필요하지 않다는 장점이 있습니다.
1. Introduction
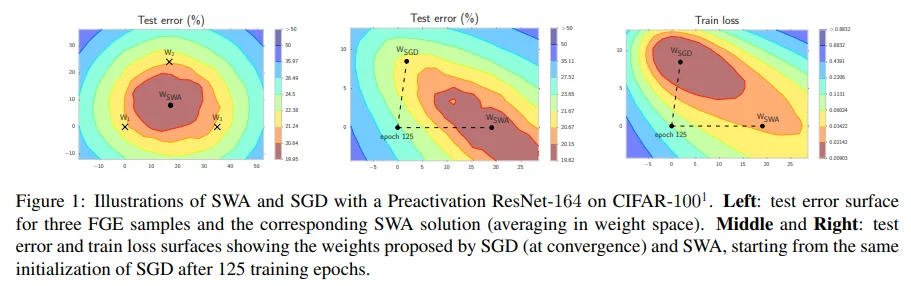
Figure 1의 왼쪽 그림을 보면 SWA solution이 test error가 낮은 지점에 위치해 있는 것을 볼 수 있습니다. 이는 model의 output ensemble 보다 weight ensemble이 더 좋을 수 있음을 보여줍니다. Weight의 평균을 다루는 비슷한 접근으로, SGD trajectory를 smooth하게 만들어주는 Exponential Moving Average (EMA)이 있지만 성능 면에서 뚜렷한 차이는 없었다고 합니다. 하지만 저자들의 SWA는 다음과 같은 장점이 있습니다.
Figure 1의 가운데/오른쪽 그림을 보면, SGD는 train loss는 좋은 위치에 있지만 test error에서 optimal point의 경계 부근에 수렴하는 모습을 보입니다. 반면,
SWA는 train loss는 좋지 않더라도 test error에서 optimal point의 중심으로 수렴하고 있습니다. 즉, SWA는 SGD보다 좋은 일반화 성능을 보이고 있습니다. (SWA의 train loss가 좋지 않은 이유는 cyclical or high constant LR로 인해 local optimum에 수렴하기에 어렵기 때문입니다.)FGE는 k번의 prediction이 필요한 반면,
SWA는 weight의 평균을 사용하여 단 한 번의 prediction으로도 FGE와 비슷한 역할을 수행할 수 있습니다.
즉, 정리하면 SWA는 cyclical or high constant LR을 적용한 SGD로 여러 weight points의 평균을 구함으로써 train loss surface를 따라 flat하고 broad한 optima을 향해 이동한다고 볼 수 있습니다.
2. Related Work
SWA는 optimization, regularization과 관련이 있습니다.
Optimization
- Keskar et al. 2017 : Batch gradient (1 batch) 방식은 sharp optima로 수렴할 가능성이 높은 반면, SGD (mini-batch) 방식은 broad local optima로 수렴할 가능성이 높다고 했습니다.
- Ruppert (1988) / Polyak and Juditsky (1992) : SGD의 weight 평균을 구하는 시초가 되는 논문으로, SWA와는 달리 train 단계에 적용했습니다.
- Exponential Moving Average (EMA) : exponentially decaying running average in combination with a decaying learning rate
Mandt et al. (2017) : 해당 논문에서 저자들이 주장한 가설에 의하면, SGD와 고정된 LR로 학습하는 것은 loss의 minimum을 중심으로 하는 Gaussian 분포로부터 sampling하는 것과 동일한 행위로 볼 수 있다고 했습니다.
- 이러한 관점에서 저자들은 SWA가 해당 구체의 중심부로 향하는 효과적인 방법이라고 했습니다.
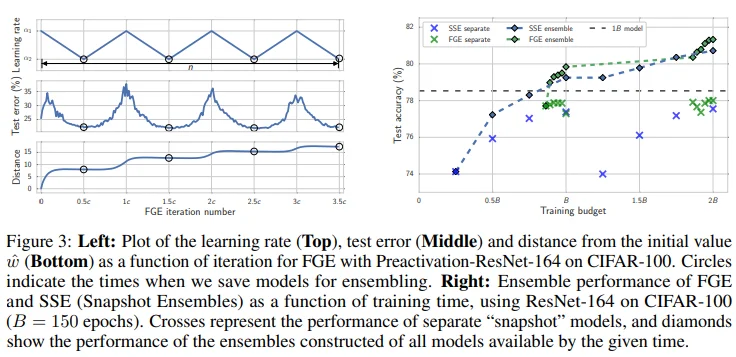
Garipov et al. (2018) (FGE) : Cyclical LR로 학습하며 ensemble에 사용할 수 있는 준수한 성능을 갖는 다양한 model들을 선택하는 방법을 제안했습니다.
Regularization
Srivastava et al. 2014 : DNN을 regularize하는 기법인 Dropout을 제안했습니다.
- 이를 본 저자들은 Dropout의 regularization 효과가 test time ensemble의 효과와 유사하기 때문에, 결국 SWA도 일종의 regularizer로 볼 수 있다고 했습니다.
3. Stochastic Weight Averaging
저자들이 말하길, SWA라는 이름에는 크게 2가지 의미가 있다고 합니다.
첫 번째는
SGD weights의 평균으로 구한다는 것이고,두 번째는
cyclical or constant LR을 적용한 SGD를 통해 stochasic weight를 얻는 loss surface 상에서의 sampling 행위로 근사될 수 있다는 것입니다.
3.1 Ananlysis of SGD Trajectories
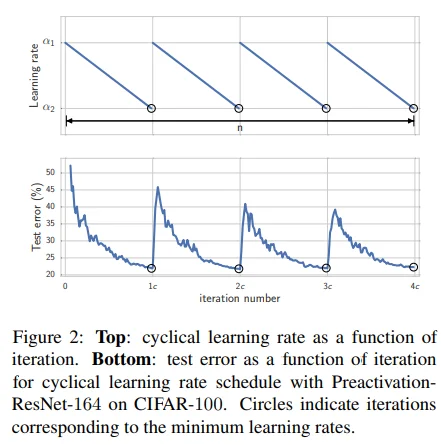
Figure 2는 cyclical LR 그래프이며, epoch가 커짐에 따라 LR이 주기적으로 감소되는 형태로 restart decaying (annealing) scheduler를 의미합니다. 또한, 기존의 연구에서 사용하던 cyclical LR과 다르게 warmup 없이 discontinuous하게 적용했습니다. 그 이유는 SWA가 단일 모델의 성능을 높이는 것이 아니라 loss surface 상에서의 exploration에 초점을 맞추고 있기 때문입니다. 위와 같은 이유로 cyclical LR과 constant LR을 비교하는 실험을 통해 LR scheduler에 따른 SGD trajectory를 확인하고자 했습니다.
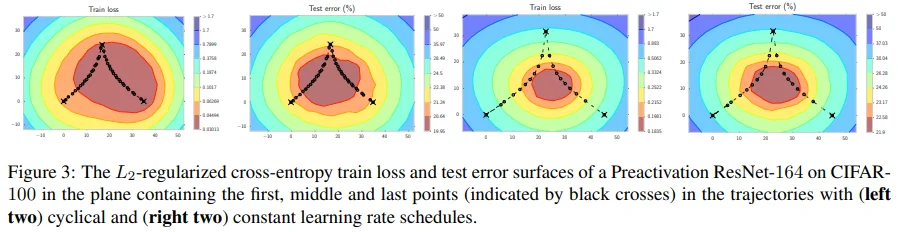
Figure 3은 train loss, test error에 대해 처음, 중간, 마지막 3개의 points가 존재하는 평면 위에 나머지 points를 투영시켜 SGD의 trajectory를 시각화했습니다.
좌측 2개 : Cyclical LR : 감소하면서 주기적으로 restart하는 LR을 사용하기 때문에 안정적으로 수렴하면서 test 성능도 좋은 편에 속합니다.
우측 2개 : Constant LR : 상대적으로 큰 LR를 사용하기 때문에 step size가 커서 test 성능은 떨어지지만, exploration 측면에서는 그 역할을 잘 수행하고 있습니다.
또한, train loss map과 test error map을 비교하면, 그 둘이 완전히 동일하지는 않더라도 상당히 유사한 형태임을 확인할 수 있습니다. 이를 근거로 저자들은 SGD trajectory를 따라 얻은 weight points들의 평균을 통해 일반화 성능을 높일 수 있지 않을까 생각하였고, 이것이 SWA의 motivation이 됩니다.
3.2 SWA Algorithm

$w_{SWA}$를 얻는 방법이 LR에 따라 약간 다릅니다.
- Cyclical LR : Figure 2에서와 같이 LR이 가장 낮은 지점의 weight로 평균을 취합니다.
- Constant LR : 각 epoch의 weight를 저장하여 평균을 취합니다.
위 방법으로 얻은 $w_{SWA}$에 대한 BatchNorm statistics update를 추가적으로 수행하면 SWA가 마무리됩니다.
3.3 Computational Complexity
SWA 사용으로 인한 memory와 time의 증가량은 크지 않다고 합니다. DNN weights의 평균을 복사해두기만 하기 때문입니다. (참고로 Network를 저장하는데 필요한 memory 연산량은 weights 자체 보다는 activation에 더 큰 영향을 받는다고 합니다.) 결과적으로 큰 규모의 netowrk에 SWA를 사용하더라도 memoty 연산량이 약 10%만 증가한다고 합니다.
3.4 Solution Width
이전의 연구들에서는 local optimum의 width가 일반화 성능과 관련이 있다고 생각했습니다. 앞서 Figure 3와 같이 Train loss와 test error는 어쩔 수 없는 shift가 존재하기 마련인데, 이때의 train loss가 broad optima로 수렴할수록 test 성능이 강건해질 것으로 여겨졌기 때문입니다.
\(w_{SWA}(t,d) = w_{SWA} + t*d\) \(w_{SGD}(t,d) = w_{SGD} + t*d\)
따라서 저자들은 $w_{SWA}$와 $w_{SGD}$ 중 어떤 방식이 더 넓은 solution을 찾는지를 확인하기 위해, $w_{SWA}$, $w_{SGD}$ 각각의 weight를 기점으로 단위 구체 상에서의 random direction vector $d$에 distance $t$를 늘려가면서 일반화 성능의 변화를 확인합니다.
- $w_{SWA}$, $w_{SGD}$ 에서 거리가 멀어지는데도 일반화 성능이 높게 유지된다면 상대적으로 더 넓은 solution을 찾았다고 볼 수 있습니다.
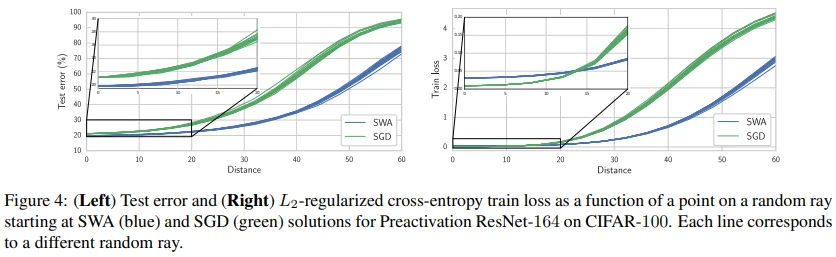
그 결과는 Figure 4에서 확인할 수 있습니다. 두 그래프 모두 초록선의 SGD보다 파란선의 SWA의 기울기가 완만하므로 SWA가 SGD보다 넓은 optima를 찾았다고 볼 수 있습니다. 다만 오른쪽의 그래프에서는 distance가 낮은 구간에서 초록선의 SGD가 더 낮은 train loss를 갖는데, 이는 앞선 실험 결과(SWA는 ensemble을 목표하기 때문에 단일 모델의 loss는 크게 중요하지 않다.)와 동일한 맥락에서 해석될 수 있습니다.
 \[w(t) = t*w_{SGD} + (1-t)*w_{SWA}\]
\[w(t) = t*w_{SGD} + (1-t)*w_{SWA}\]
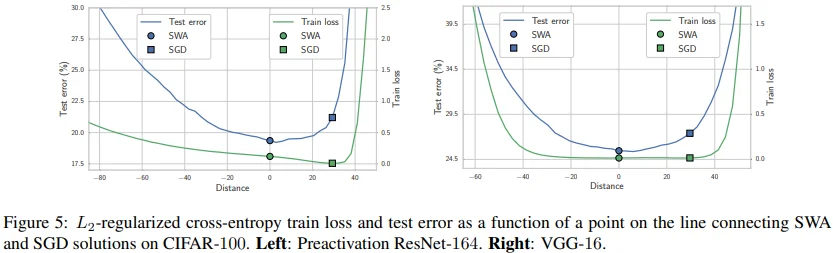
Figure 5는 $w(t)$를 시각화한 그래프입니다. 여기서도 앞에서 언급되었던 train loss와 test error 사이에 어쩔 수 없이 존재하는 shift 개념, 상대적으로 더 낮은 $w_{SGD}$의 train loss와 같은 내용들을 확인할 수 있습니다. 또한, 상대적으로 $w_{SWA}$에 비해 $w_{SGD}$가 가장자리에 위치하기 때문에 train - test 사이의 shift에 큰 영향을 받게 되고, 이로 인해 $w_{SGD}$가 $w_{SWA}$보다 낮은 일반화 성능을 갖는 것으로 해석할 수 있습니다.
한편, 이러한 관찰을 근거로 Keskar et al. (2017) 논문이 잘못된 결론에 도달한 이유를 설명합니다. 해당 논문의 저자들은 large batch로 학습한 SGD의 solution에 존재하는 sharp optima는 사실 대부분의 directions이 flat하지만 일부 direction에서 극도로 가파르다고 주장했습니다. 이러한 sharpness에 대한 잘못된 추측으로 인해 그들은 small batch SGD 보다 large batch SGD의 일반화 성능이 부족하다는 결론을 내리게 됩니다. 하지만 Figure 4, 5를 보면 (small batch) SGD 또한 일반화 성능의 하락을 유도할 만한 정도의 가파른 경계에 위치하는 것을 볼 수 있습니다. (그런데 SGD가 SWA에 비해 가파를 뿐이지, 언급한 연구를 했던 저자들의 결론이 잘못되었다고 할 수 있는지.. 잘 모르겠습니다.)
3.5 Connection to Ensembling
Garipov et al. (2018)에서 제안한 FGE는 cyclical LR로 weight space 상에서 좋은 성능의 유사한 point들을 찾아내고 이를 바탕으로 여러 output을 구합니다. 반면 SWA는 weight point들을 ensemble하여 단 하나의 output을 도출하는 방식임에도 불구하고 FGE를 수학적으로, 실험적으로 잘 근사한다는 내용을 증명했습니다. (자세한 내용은 논문을 참고해주세요.)
3.6 Connection to Convex Minimization
Sampling
Mandt et al. (2017)에서 fixed LR를 사용한 SGD는 마치 loss의 minimum을 중심으로 Gaussian 분포에서 sampling하는 것과 같다고 했습니다. 이때 SGD로부터 얻어지는 sample을 $w_i$ / local minimum을 $\hat w$이라 하면, 이를 $w_i$ ~ $N(\hat w, \Sigma)$ 로 표현할 수 있습니다. 여기서 k가 무한대로 증가함에 따라 $w_{SWA}$는 $\hat w$으로 수렴하는 것이 보장된다고 합니다.
Convex Minimization
일반적으로 DNN loss 함수는 non-convex하다고 알려져 있지만, SGD trajectory 상에서는 convex한 것으로 근사될 수 있다고 합니다. 하지만 Figure 5에서처럼 SWA가 train loss의 중심부로 잘 수렴하는 것을 보면, loss 함수가 locally non-convex 성질을 갖더라도 SWA는 준수한 일반화 성능을 보장할 수 있습니다. (SWA는 SGD trajectory 상에서 averaging 연산을 통해 실제로 가보지 못한 weight로 update 될 수 있기 때문에, loss 함수의 수렴성을 판단하는 convex 개념이 중요하지 않은 것으로 보인다.)
4. Experiments
4.1 CIFAR Datasets
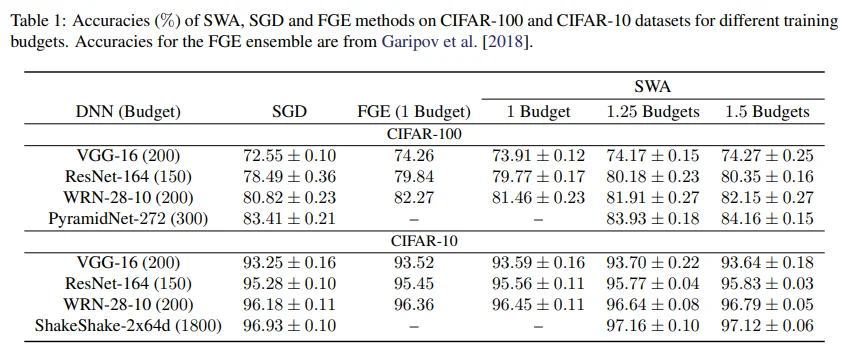
Table 1에 등장하는 Budget은 SGD 훈련 과정에서 수렴되었다고 판단되는 epoch를 의미합니다. 먼저 SWA를 보면 훈련 epoch를 늘렸을 때 성능 향상이 존재하는 것을 확인할 수 있습니다. SWA 학습 과정은 각 모델별로 약간 다르긴 하지만, 먼저 SGD로 0.75 ~ 1.0 Bugdet을 학습한 후에 추가로 0.25 / 0.5 / 0.75 Budget 만큼 SWA로 학습했습니다.
다시 Table 1을 보면, SGD와 동일한 1 Budget 학습에서 SWA의 성능이 확실히 더 높고, 여러 번 inference를 수행하는 FGE 방식과 비교했을 때에도 WRN-28-10 모델을 제외하면 SWA의 성능이 약간 더 높은 것을 확인할 수 있습니다.
4.2 ImageNet
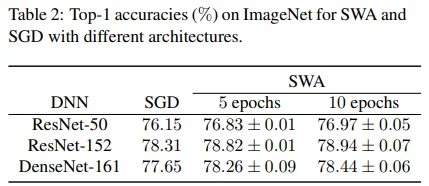
Torchvision에서 제공하는 pretrained model에 5 / 10 epoch 동안 SWA 학습을 시켰더니 약 0.6 ~ 0.9 % 점수가 상승하였습니다.
4.3 Effect of the Learning Rate Schedule
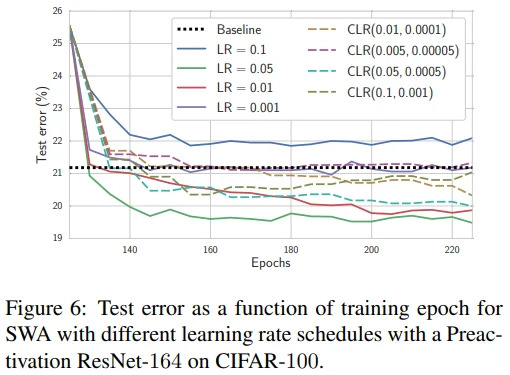
다양한 LR schedule의 결과를 확인해보기 위해 125 epoch 까지는 동일한 방식으로 SGD를 사용했고, 이후 적용되는 LR와 schedule 방식을 다르게 적용했습니다. Constant LR을 사용했을 때, 수렴 속도가 빠르고 Test error도 더 낮은 것을 확인할 수 있습니다.
4.4 DNN Training with a Fixed Learning Rate
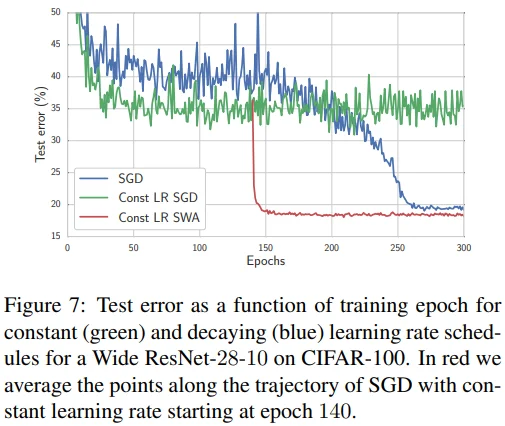
- Blue : SGD / Cyclical LR 학습
- Green : SGD / Constant LR 학습
- Red : Green과 동일하나, 140 / 300 epoch 에서 wegiht average 수행
정리하면, SGD는 constant LR을 사용할 때 진동하지만 같은 조건에서 SWA는 수렴할 수 있습니다. 또한, fixed LR로 학습할 수 있다는 것은 SWA의 중요한 특징 중 하나입니다. 마지막으로, SWA 학습을 위해 scratch부터 학습하는 것보다 conventional training으로 pretrained model을 사용하는 것을 추천합니다.
5. Discussion
결론은 한 번 읽어보는 것이 좋다고 생각해서 그대로 인용했습니다.
We have presented Stochastic Weight Averaging (SWA) for training neural networks. SWA is extremely easy to implement, architecture-agnostic, and improves generalization performance at virtually no additional cost over conventional training.
There are so many exciting directions for future research. SWA does not require each weight in its average to correspond to a good solution, due to the geometry of weights traversed by the algorithm. It therefore may be possible to develop SWA for much faster convergence than standard SGD. One may also be able to combine SWA with large batch sizes while preserving generalization performance, since SWA discovers much broader optima than conventional SGD training. Furthermore, a cyclic learning rate enables SWA to explore regions of high posterior density over neural network weights. Such learning rate schedules could be developed in conjunction with stochastic MCMC approaches, to encourage exploration while still providing high quality samples. One could also develop SWA to average whole regions of good solutions, using the high-accuracy curves discovered in Garipov et al. [2018].
A better understanding of the loss surfaces for multilayer networks will help continue to unlock the potential of these rich models. We hope that SWA will inspire further progress in this area