[논문리뷰] VQ-VAE: Neural Discrete Representation Learning (NIPS ‘17)

10 May 2023 in Papers / Review

Abstract

먼저, VAE와 VQ-VAE의 차이점은 아래와 같이 정리할 수 있습니다.

VAE : continuous latent + gaussian prior

VQ-VAE : discrete latent + learnable categorical prior

이렇게 VQ-VAE가 discrete latent 학습이 가능했던 이유는 vector quantisation (VQ) 덕분입니다.

그리고 VQ를 사용함으로써 VAE의 posterior collapse 현상도 방지할 수 있게 되었습니다. 참고로, VQ-VAE 논문에서는 posterior collapse란 (powerful) autoregressive decoder가 decoding 과정에서 latent 정보가 무시되는 현상으로 정의하고 있습니다.

좀 더 원론적으로 표현하면, posterior collapse는 VAE의 objective인 ELBO 중에서 regularization error term에 의해 발생하며, approximate posterior와 gaussian prior z가 같아지는 현상입니다.

마지막으로, VQ를 활용하여 discrete latent variables을 얻은 다음, autoregressive model(PixelCNN, WaveNet)에 넣어주면 autoregressive prior를 얻을 수 있는데, 이를 통해 높은 퀄리티의 image, video, speech를 생성할 수 있다고 하네요. (autoregressive 관련해서는 3.3 prior 및 4. Experiments 에서 다룰 예정입니다.)

1. Introduction

Motivation

VLAE 논문에서 log-likelihood로 최적화되는 생성 모델은 latent 개념 대신 PixelCNN처럼 강력한 decoder가 필요할 것이라는 추측을 했다고 합니다. (읽어보진 않았지만 VAE의 저자 Kingma님이 참여하신, VAE를 이해하는데 중요한 논문으로 보였습니다.)

하지만, VQ-VAE의 저자들은 likelihood로 최적화하더라도 딥러닝 모델은 latent space에 유의미한 feature들을 뽑아낼 수 있다고 생각했습니다. 또한, discrete latent가 여러 modality에 잘 어울릴 뿐만 아니라 추론, 계획, 예측 등의 학습에도 유리하다고 생각했다네요.

당시 latent space는 continuous (like VAE) 하거나 discrete 했는데, 앞서 언급된 장점에도 불구하고 discrete latent에서는 성능이 잘 나오지 않았습니다. 이러한 배경에서 저자들은 WaveNet을 참고하여 discrete latent와 autoregressive model을 활용해보기로 합니다. (참고로 PixelCNN, WaveNet, VQ-VAE 저자가 모두 같습니다.)

물론 VQ-VAE 이전에도 discrete latent를 학습하기 위한 NVIL 논문, VIMCO 논문이 존재했고, 새로운 parametrization 기법을 제안하는 Concrete distribution 논문, Gumbel-softmax 논문도 존재했습니다. 하지만 이들은 VAE만큼 성능이 잘 나오지 않았다고 합니다.

또한, VQ-VAE는 autoregressive distribution을 VAE의 decoder나 prior와 연관지어 사용할 수 있음을 밝혔습니다.

마지막으로, vector quantisation은 image compression 분야와도 관련이 있다고 언급하고 있습니다.

3. VQ-VAE

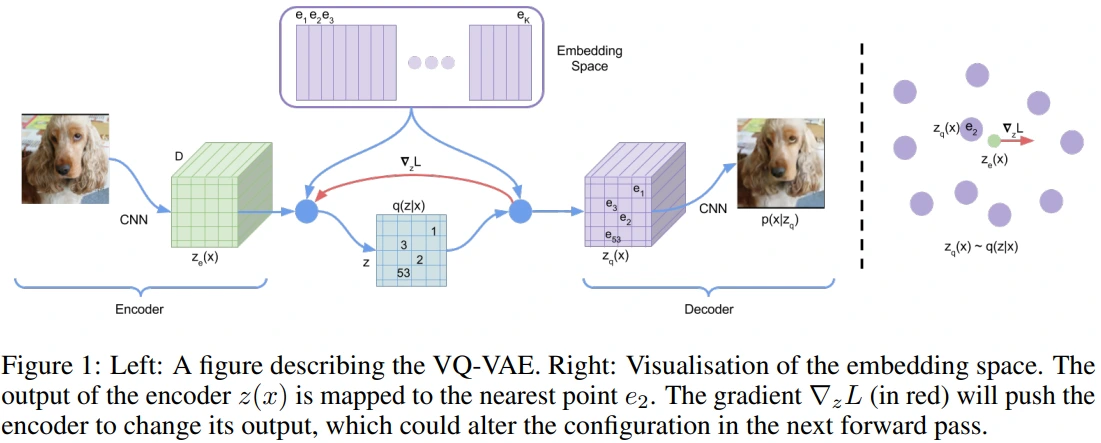
참고로 맨 오른쪽 그림에서 빨간색 화살표의 방향에 큰 의미는 없고, decoder로부터 encoder로 gradient가 흐른다는 부분을 강조하기 위함입니다.

3.1. Discrete latent variables

아래 수식은 posterior categorical distribution $q(z\mid x)$를 표현한 식입니다. 즉, encoder $z_e(x)$와 가장 가까운 임의의 embedding 1개만 구함으로써, 각각의 latent vector들이 discrete embedding space에 mapping될 수 있습니다. 그리고 이러한 mapping이 vector quantisation (VQ) 이라고 생각하셔도 될 것 같습니다.

eq1

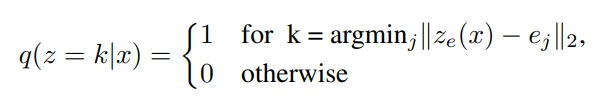
즉, VAE의 variational inference를 적용한 approximate posterior가 간단히 VQ로 대체됩니다. 이를 수식적으로 objective 측면에서 바라본다면, VQ-VAE에서는 ELBO의 regularization term인 KLD가 상수값이 되기 때문에 posterior collapse 문제로부터 자유로워지는 것을 확인할 수 있습니다.

$ELBO = likelihood - KLD = E_{z\sim q(z\mid x)}[\log p(x\mid z)] - D_{KL}[q(z\mid x)\mid p(z)]$
$q(z\mid x)$ = one-hot distribution (VQ)
$p(z)$ = categorical distribution

아래 수식은 encoder의 output과 가장 가까운 embedding이 그대로 decoder의 input으로 처리되는 과정을 나타냅니다. 이 과정에서 gradient를 계산하는 과정은 없지만, 수학적으로 이러한 approximate를 straight-through estimator와 유사하다고 서술하고 있습니다.

$z_q(x) = e_k$, where $(k=argmin_j \mid \mid z_e(x)-e_j \mid \mid _2)$

참고로 latent의 차원에 제한사항이 없기 때문에, 각 modality의 특성에 맞게 1D(Speech), 2D(Image), 3D(Video) latent space를 사용하였습니다.

3.2. Learning

$L = \log p(x\mid z_q(x)) + \mid \mid sg[z_e(x)]-e\mid \mid ^2_2 + \beta \mid \mid z_e(x)-sg[e]\mid \mid ^2_2$
$L$ = reconstruction loss + embedding loss + commitment loss
$z_e(x)$ : encoder output
$z_q(x)$ : decoder output
sg : stop gradient
e : embedding

Reconstruction loss는 의미상 VAE와 동일합니다. 다만 VQ-VAE에서는 MAP inference 과정에 VQ를 적용한다면, (충분한 학습을 통해 수렴한 경우) z 중에서 $z_q(x)$인 경우만 고려되는 것을 알 수 있습니다.

최종적으로 아래 3번째 line의 $\log p(x\mid z_q(x))$가 reconstruction loss가 됩니다. 이를 구현할 때에는 MSE loss를 사용하였는데요. 이유가 궁금하시다면 이 글을 참고하시면 좋을 것 같습니다.

$\log p(x) = \log \Sigma_{k}p(x\mid z_k)p(z_k)$
$\log p(x) \approx \log p(x\mid z_q(x))p(z_q(x))$ , by VQ
$\log p(x) \geq \log p(x\mid z_q(x))p(z_q(x))$ , by Jensen’s inequality

Embedding loss는 embedding vector를 학습하는 loss로, encoder output을 target으로 l2 error를 minimize합니다.

Commitment loss는 정확히 embedding loss와 반대로 되어 있으며, $\beta$라는 coefficient로 값이 조절되는 구조로 $\beta$ 값에는 크게 영향을 받지 않는다고 합니다.

Commitment loss가 필요한 이유는 embedding space가 dimensionless하기 때문이라고 언급하고 있는데요. 사실 잘 와닿지는 않았고, 이 글을 보면서 약소하게나마 이해할 수 있었습니다. 요약하면 reconstruction loss를 통해 각각의 이미지로부터 얻는 latent 간 거리가 멀어지게 될텐데, 이렇게 멀어지는 latent를 embedding vector가 쫓아가는 식으로 학습하다보면 (VQ loss), embedding vector가 dimensionless하기 때문에 어느 정도의 제한이 필요하다는 내용입니다.

3.3. Prior

VQ-VAE 학습 과정에서 p(z)는 VQ에 의해 categorical 분포를 따르게 됩니다. 여기에 저자들은 autoregressive model을 활용하여 pretrained VQ-VAE latent로부터 autoregressive prior를 학습할 수 있도록 하였습니다. 최종적으로 autoregressive prior로부터 ancestral sampling을 통해 latent code를 생성하고 이를 decoding 함으로써 generative model로 기능할 수 있도록 설계했습니다.

조금 더 구체적으로는, 학습이 끝난 VQ-VAE의 latent를 input으로 받아서 autoregressive model에 넣어주는 방식인데요. 재미있는 부분은 autoregressive prior 학습에 사용되는 cross-entropy loss의 target이 input과 동일하다는 점입니다. 즉, input과 output은 동일하지만 그 안에서 autoregressive하게 표현하는 것을 학습하도록 설계를 했습니다.

Autoregressive model은 PixelCNN(이미지), WaveNet(오디오)을 사용하였으며, 저자들은 prior와 VQ-VAE를 jointly하게 학습하면 더 좋지 않을까 하는 future work도 제안합니다.

4. Experiments

4.1. Comparison with continuous variables

VQ-VAE(4.67)는 VAE(4.51)보다는 낮지만 VIMCO(5.14)에 비해 꽤나 괜찮은 성능을 보였습니다.

bits/dim metric을 사용하였는데, 이는 negative_log_likelihood / # of pixels 라고 생각하시면 됩니다. 이 값이 낮을수록 좋습니다.

4.2. Images

Figure 2에서 VQ-VAE의 reconstruction 결과를 보면, 원본 이미지보다 약간 blurry한 것을 볼 수 있습니다. 이는 정보의 압축율이 약 42.6에 달하는 것에 비하면, latent가 원본 이미지의 특징들을 잘 추출하고 있다고 생각해볼 수 있습니다.

압축률은 input 차원 / latent 차원 이라고 생각하셔도 좋을 것 같습니다. 먼저, 분자와 분모에서 앞쪽 3개의 값은 각각 input image와 z의 차원을 의미합니다. 또한, 분자의 8은 pixel의 8bit를 의미하고, 분모의 9는 embedding의 개수인 K(=512)와 관련이 있습니다.

압축률 수식은 다음과 같습니다. $\frac{128*128*3*8}{32*32*1*9} \approx 42.6$

input image shape = (128, 128, 3)
z shape = (32, 32, 1)
$log_2(256)$ = 8
$log_2(K)$ = $log_2(512)$ = 9

Figure 3과 Figure 4는 PixelCNN prior에서 sampling한 후 VQ-VAE decoder로 생성한 결과입니다.

Figure 3은 ImageNet으로 PixelCNN prior를 학습하였고,

Figure 4는 DeepMind Lab 환경에서 얻은 이미지로 PixelCNN prior를 학습하였습니다. 참고로 reconstruction 결과는 없지만, 원본 이미지와 거의 동일했다고 합니다.

PixelCNN prior는 pretrained VQ-VAE의 encoder로 latent를 추출한 다음, 이 latent를 PixelCNN의 input이면서 동시에 cross-entropy loss의 target으로 설정하여 학습시킵니다. (직관적으로는 VQ-VAE의 latent를 PixelCNN으로 autoregressive하게 표현하는 과정을 학습한다고 생각합니다.) 마지막으로 PixelCNN prior에서 sampling한 z를 VQ-VAE decoder에 태워서 generation을 수행하게 됩니다.

이러한 방식을 사용할 경우, training 및 sampling 속도가 향상되고, global structure를 caputer할 수 있는 PixelCNN의 장점을 가져올 수 있다고 언급하고 있습니다.

마지막 실험은 조금 복잡한데요. 먼저, Figure 4의 first pretrained PixelCNN prior에서 추출한 latent를 PixelCNN decoder에 태워서 학습한 것으로 보입니다. 그 다음, 학습이 끝난 second PixelCNN prior에서 얻은 latent를 VQ-VAE decoder에 태워서 reconstruction을 수행한 것으로 보입니다. (솔직히 맞는 해석인지는 잘 모르겠네요..) 참고로 latent variable은 3개 사용했다고 하는데요. 그 이유로는 reconstruction 결과가 좋지 않았을 것으로 의심되고, latent 3개를 사용한다면 구체적으로 어떻게 작동하는지 의문이 있습니다. (평균을 낸다거나, 3개의 결과 중 좋은 것을 선택한다거나 할 수도 있을 것 같습니다.)

어쨌든 위 실험을 통해 저자들이 말하길, VAE에서는 powerful decoder(PixelCNN decoder)를 사용할 때 posterior collapse 현상이 나타났는데, VQ-VAE에서는 powerful decoder를 사용하더라도 latent가 고유한 의미를 가질 수 있었다고 주장하고 있습니다.

4.3. Audio

이번에는 audio domain에 대한 실험입니다. 참고로 WaveNet deocder와 유사하게 dilated convolution layer를 VQ-VAE에 적용했고, input waveform 대비 64배 줄어든 latent를 512개 갖도록 구성했습니다. Decoder는 latent뿐만 아니라 speaker에 대한 one-hot embedding에 condition되었다고 하는데, 아마도 이 condition을 통해 특정 speaker에 대한 VQ-VAE의 audio generation 성능을 확인하고자 한 것 같습니다.

첫 실험으로 저자들은 VQ-VAE가 long-term relevant information을 잘 추출할 수 있는지를 확인하고자 했습니다. (쉽게 말하면, long-term에 걸쳐 sample이 가진 정보를 latent에 담아낼 수 있는지를 확인했다고 할 수 있습니다.) 실험 결과, input 대비 64배 만큼 축소된 latent로 reconstruction하다보니 input과 완전히 동일한 output을 얻지는 못했습니다. 하지만 이러한 변화는 약간의 차이에 그칠 뿐, speech에 담긴 text는 온전히 복원되었다고 합니다. 즉, VQ-VAE는 encoding에 대한 어떠한 supervision이 없었음에도 latent space에 speech content를 성공적으로 encoding 할 수 있었습니다.

두번째 실험으로 unconditional sample에 대한 실험을 했습니다. 여기서는 앞의 실험에 비해 speaker가 더 많은 dataset을 사용했고, input 대비 128배 만큼 축소된 latent를 사용했습니다. (전체적인 실험 세팅이 앞의 실험보다는 어렵다는 것을 확인할 수 있습니다.) 실험 결과는 WaveNet보다 VQ-VAE의 sound가 더 clear 했다고 합니다.

세번째 실험으로 speaker conversion 성능을 확인했습니다. Speaker conversion의 방식으로 어떤 speaker로부터 추출된 latent와 함께, 다른 speaker id를 condition으로 decoder에 태워서 복원을 진행했다고 하는데요. 이렇게 얻은 synthesised speech는 original과 동일한 content(text)를 가지면서, speaker id에 해당하는 voice가 입혀지는 결과를 얻었다고 합니다.

마지막 실험에서는 7.2%의 정확도를 기록한 random latent space와 비교하여 VQ-VAE의 latent로는 49.3% 정도의 성능을 보였다고 합니다.

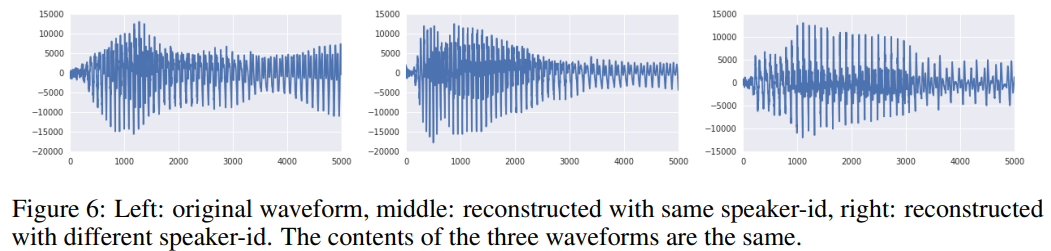
Figure 6를 보면, 모두 동일한 content를 가진, 각기 다른 형태의 waveform을 확인할 수 있습니다.

4.4. Video

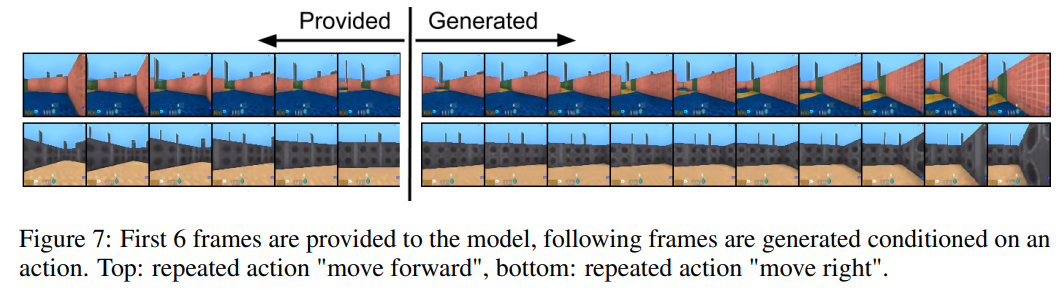
마지막으로 Figure 7은 video domain에 대한 실험입니다. Action을 condition으로 제한하고, action sequence 6 frames를 VQ-VAE에 학습시켜, 학습된 VQ-VAE로부터 sampling을 통해 10 frame을 생성하는 방식으로 설계되었습니다. 위 figure를 통해 실험 결과를 확인할 수 있습니다. (1행은 move forward, 2행은 move right을 수행하고 있는 frame입니다.) 저자들이 밝히길 action에 대한 condition 없이 action sequence만으로 학습해도 위와 비슷한 결과를 얻었다고 합니다.

5. Conclusion

VQ를 적용하여 VAE의 latent space를 discrete하게 바꾼 VQ-VAE 제안
VAE + discrete latent 분야의 이전 연구들과의 차이점 : VAE와 성능이 비슷 (Chapter 4.1)
Image, Audio, Video domain의 다양한 task에서 유의미한 수준의 성능 확인

[논문리뷰] VQ-VAE: Neural Discrete Representation Learning (NIPS ‘17)

Abstract