[논문리뷰] DALL-E: Zero-Shot Text-to-Image Generation (ICML ‘21 Spotlight)

12 Jun 2023 in Papers / Review

arXiv link

github link

---

요약

• Text 및 Image token(=dVAE encoder output)을 input으로 받아, autoregressive하게 next Image token을 예측하며, 이 token들을 모아 dVAE decoder에 태워 T2I generation task 수행

• 큰 모델에 충분한 양의 데이터로 학습하면, zero-shot 평가에서도 domain-specific 모델만큼의 성능을 보인다.

• 12B transformer 모델의 경제성을 위한 고민들 (Sparse attention, Mixed precision training, Distributed optimization 등)

(수식 표현이 이상한 경우에는 새로고침 해주세요.)

---

2. Method

저자들의 목표는 transformer 구조를 활용해서 text, image token을 single stream으로 autoregressive하게 학습하는 것입니다.

그렇다면 왜 이미지 pixel이 아니라 token이냐? 이미지의 pixel을 그대로 사용하는 경우 메모리가 매우 많이 필요하고, (PixelCNN++에서 밝힌) high-frequency detail에 모델의 학습이 편향됩니다. 그래서 dVAE encoder로 이미지 token을 얻기 위해 2 stage 학습을 합니다. (순서: dVAE -> prior)

Stage 1에서는 dVAE를 학습합니다. 이때 Encoder는 이미지를 token grid로 압축하면서 (256x256x3 -> 32x32), 이 과정에서 손실되는 정보량을 보완하기 위해 codebook size를 큰 값(K=8192)으로 정했습니다. 아래의 figure 1을 통해 디테일은 부족하지만, token으로 압축되더라도 이미지 복원이 충분히 가능함을 확인할 수 있습니다.

Stage 2에서는 BPE-encoded text token 256개와 dVAE-encoded image token 1024개(=32x32)로 image-text joint 분포를 transformer 모델이 학습하게 됩니다.

생성 과정은 수식을 통해서 확인해볼 수 있습니다.

먼저, 각 module이 modeling하는 분포에 대한 설명입니다.

• $q_{\phi}$ : dVAE encoder (modeling generated image tokens given RGB images)
• $p_{\theta}$ : dVAE decoder (modeling generated RGB images given image tokens)
• $p_{\psi}$ : transformer (modeling joint distribution with text and image)

다음은 생성 모델의 동작 방식을 표현한 수식과 objective인 ELBO 입니다.

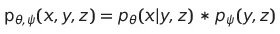
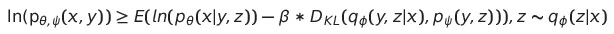
• $x$ : image
• $y$ : caption
• $z$ : token

위 식에서 $\beta$는 beta-VAE에서 도입된 것입니다.

참고로, $\beta$를 통해 reconstruction과 regularization(= latent 내 disentanglement)을 조절할 수 있다고 알려져 있습니다. $\beta$가 커질수록, latent code가 disentangle 될 수 있다고 하네요.

2.1. Stage One: Learning the Visual Codebook

대략적으로 아래의 flow로 처리되며, Official repo에서는 num_tokens와 codebook_dim을 같게 두었습니다.

input = (B,3,256,256)

-> encoder output = (B,K=8192,32,32)

-> gumbel-softmax output = (B,K=8192,32,32)

-> codebook output = (B,codebook_dim=8192,32,32)

-> output = (B,3,256,256)

dVAE encoder

저자들은 transformer의 initial prior $p_{\psi}$가 codebook vector(K=8192)(=logit)에 대한 uniform categorical 분포를 따른다고 설정하였습니다. 이러한 설정을 통해 ELBO 식에서 KL divergence를 계산할 수 있게 되고, 의미론적으로는 encoder output(=logit)이 uniform 분포와 가까워짐으로써 gumbel-softmax를 통해 다양한 token이 선택되어 결국 codebook의 표현력을 높일 수 있었다고 생각합니다.

그리고 $q_{\phi}$는 32x32 grid 각각의 채널이 8192인 logit을 parameter로 하는 categorical 분포를 따른다고 설정하였습니다. 하지만 이렇게 설정하면 backpropagation이 어렵게 되죠. 이러한 문제를 해결하고자 VQ-VAE에서는 VQ라는 straight-through estimator를 적용하였지만, dVAE에서는 gumbel-softmax relaxation을 적용했습니다.

• (뇌피셜) DALL-E에서 VQ 대신에 gumbel-softmax를 사용한 이유는 뭘까?

  • T2I 모델이라서? DALL-E에서는 text, image token을 바탕으로 예측된 image token을 모아 decoding하는데, VQ로 학습한 decoder로는 multi-modality가 반영된 token을 다루기 힘들지 않았을까 추측됩니다.

  • 단순히 여러 parameter에 대한 실험이 가능해서? torch gumbel-softmax 구현체를 보니, soft/hard 전환도 쉽고 tau라는 parameter도 있어서, 더 많은 실험이 가능했을 것 같습니다.

참고로, relaxation parameter인 $\tau$ 값이 0에 가깝게 작아질수록 one-hot vector와 가까워지고, 커질수록 uniform 분포와 가까워집니다. (참고: Gumbel-Softmax 리뷰)

dVAE decoder

dVAE decoder가 modeling하는 $p_{\theta}$의 likelihood는 log-laplace 분포를 사용했습니다. 그 이유는 아래의 Appendix A.3 The Logit-Laplace Distribution에서 확인할 수 있습니다.

• decoder 학습에 관여하는 reconstruction loss는 일반적으로 L1 or L2 objectvie를 사용합니다. 이는 decoder가 modeling하는 분포가 각각 laplace, gaussian 분포인 경우를 가정하고 있습니다.
• 하지만 pixel value는 0~255 사이에 속하기 때문에 이러한 분포 가정이 mismatch라고 주장하며, 저자들은 pdf가 (0,1)에서 정의되고 µ와 b를 parameter로 갖는 logit-Laplace distribution을 제안하였습니다.
• 이는 dVAE 학습 과정에서 reconstruction term 계산에 사용되며, dVAE decoder의 output feature map 6개 중 3개는 µ parameter를, 나머지 3개는 b parameter를 구하는 데 사용된다고 합니다.
• 마지막으로, 해당 pdf의 분모에 x*(1-x) term이 존재하여, input value scope [0, 255] 대신 (e, 1-e)를 사용하였으며 e는 0.1을 사용했다고 합니다.

for stability

또한, dVAE 학습의 안정성을 위해 저자들이 중요하게 생각했던 부분은 다음과 같습니다.

• Annealing schedule

  • relaxation parameter인 $\tau$ 값을 1에서 1/16로 annealing하면, relaxed ELBO와 true ELBO 사이의 gap이 거의 없었다고 합니다. (참고: Appendix A.2. Training)

• 1x1 convolution (encoder 마지막, decoder 처음)

  • encoder와 decoder 구성에서 conv의 hidden dim을 줄여놓고 마지막에 1x1 conv로 channel을 키워줄 때, true ELBO에 대한 일반화가 잘 되었다고 합니다.

• activation

  • 아마도 1x1 conv를 적용하기 전에 activation을 한 번 더 적용할 때, 초기 안정성에 도움이 된다는 내용으로 보입니다.

마지막으로, KL weight $\beta$를 6.6으로 키웠을 때 codebook 활용도가 좋으면서, 학습이 끝났을 때 reconstruction error가 매우 낮아졌다고 합니다.

이는 앞서 언급했던 $\beta$의 reconstruction-regularization trade-off 개념과는 다른 결과입니다. 이를 두고 저자들은 $\beta$ 값이 작은 경우, 학습 초기에 relaxation noise가 codebook 활용도를 낮춰 ELBO 수렴이 좋지 않았을 것으로 추측하고 있습니다.

2.2. Stage Two: Learning the Prior

Stage 2에서는 $\phi$와 $\theta$를 fix 시켜놓고, text & image token을 input으로 transformer decoder로 $\psi$를 modeling합니다.

• Text token : BPE-encoding (10% BPE dropout), 최대 256 token, 16384 vocab size

• Image token : dVAE-encoding, 1024 token, 8192 vocab size

  • stage 2에서는 dVAE logit에 argmax sampling만 적용 (gumbel noise X)

  • ImageNet 실험 결과 overparameterized regime에서는 기존 sampling 방식이 useful regularizer의 기능을 했는데, DALL-E stage 2는 underparameterized regime여서 큰 상관 없을 것이라고 판단했다고 합니다.

    • (뇌피셜) dataset과 model이 크기 때문에 underparameterized regime라고 판단한 것으로 추측됩니다.

embedding

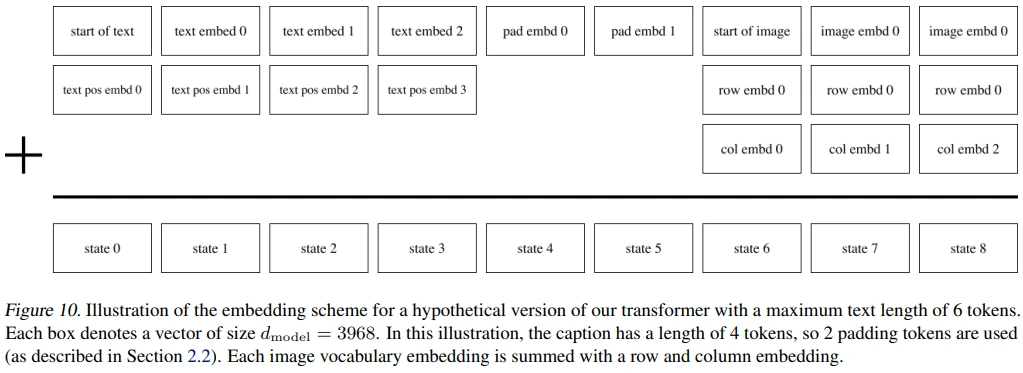
Figure 10처럼 text token + pad token + image token 의 순서로 concat 되며, text token에 positional embedding, image token에 row & column embedding이 적용됩니다. 이처럼 pad token을 적용할 경우, Conceptual Captions 논문에 따르면 validation loss는 높아지지만, OOD caption에 대해 좋은 성능을 보인다고 합니다.

sparse attention

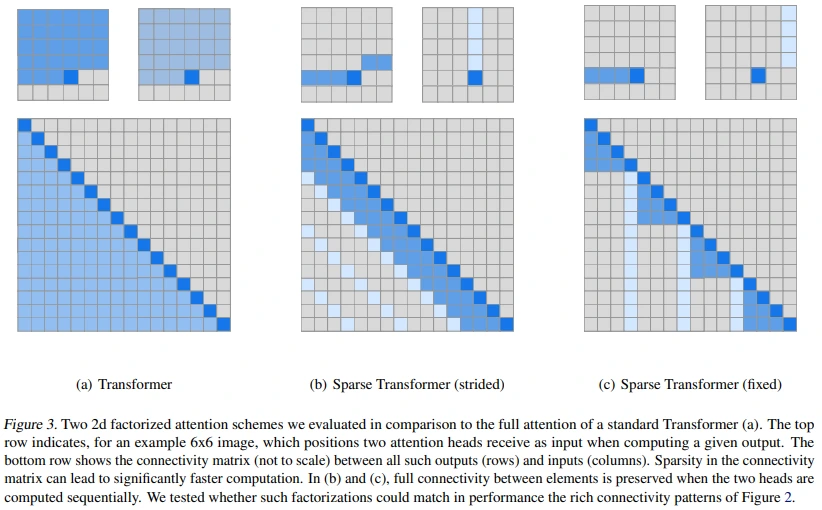
Transformer decoder에서 사용한 sparse attention mask는 총 64개 layer에 (row + column + [row + row + row + column] * 15 + row + conv) 순서로 적용되었습니다.

참고로, 아래의 sparse attention mask의 대전제는 각 image token이 모든 text token에 attention 될 수 있는가 였습니다.

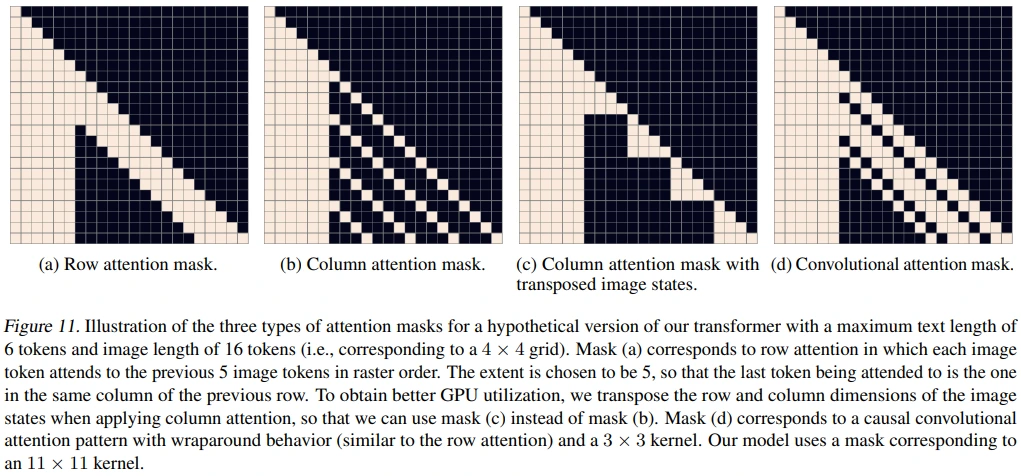
figure 11은 6 text token + 16 image token을 예시로 하는 경우로, text / image token이 아래와 같은 형식으로 concat된 결과입니다.

• Text-to-text attention : standard attention mask
• Image-to-image attention : row, column, or convolutional attention mask

각 예시에 대한 설명은 다음과 같습니다.

• (a) Row attention mask

  • row 1개의 길이보다 1만큼 더 attention 했습니다. (예시 기준, 4 + 1 = 5)
  • 그 이유는 previous row의 same column token까지 attention에 추가하기 위함입니다.

• (b) Colmun attention mask

  • (b)는 GPU 활용도가 낮기 때문에 (c)를 고안하여 사용했습니다.

• (c) Column attention mask with transposed image states

  • (b)에서 row와 column을 trasnpose하면 (c) 형태로 나타난다고 합니다.
  • 아래의 Sparse Transformer의 figure를 참고하시면 이해되실 것 같습니다.

• (d) Convolutional attention mask

  • (d)는 3x3 kernel을 사용한 예시로, DALL-E에서는 11x11 kernel을 사용했습니다.

마지막으로, DALL-E는 image 생성 모델이기 때문에, cross-entropy loss 비율을 text(1) : image(7)로 적용하였습니다.

2.3. Data Collection

저자들은 인터넷으로부터 250M 규모의 text-image pair dataset을 구축했습니다.

• MS-COCO train 포함 X (YFCC100M에 포함된 MS-COCO 이미지는 일부 포함될 수 있음)
• Conceptual Captions 포함
• YFCC100M 중 filtered subset 포함
• Wikipedia

자세한 과정은 Appendix C. Details for Data Collection, Conceptual Captions 논문, DALLE-datasets 레포를 참고하시면 도움되실 것 같습니다.

2.4. Mixed-Precision Training

DALL-E(12B)보다 작은, 소규모 모델(1B)의 학습 과정에서 GPU 메모리 관리 및 throughput 향상을 위해 다음의 3가지를 설계했습니다.

• 모델 parameter의 대부분, Adam moment, activation을 16bit precision로 저장
• 시간 손해는 있지만 메모리 이점이 있는 activation checkpointing 적용
• 각 transformer block의 backward process에서 activation recompute

그런데 학습 과정에서 수렴하지 못하는 현상을 발견하였고, 저자들은 16bit precision에서 야기된 underflow 현상을 그 원인으로 보았습니다.

per-resblock gradient scaling

다음으로 해결책 중 하나였던 per-resblock gradient scaling에 대해 설명하겠습니다.

저자들은 Admin 논문에서와 유사하게, 앞쪽 block에서 뒤쪽 block으로 전달되는 activation gradient의 norm이 감소하여 underflow 현상이 생겼습니다. (Admin에서 제안하는 initialization을 적용해보았으나 효과는 없었다고 하네요.)

기존의 Mixed precision training에서는 smallest, largest activation gradient로 range를 shift하여 이러한 underflow 현상을 극복하려 했습니다. 이는 동일한 크기의 language model 학습을 가능하게 하였지만, text-to-image model (DALL-E)에서는 range가 너무 작았다고 하네요. (표현이 애매하지만, 결론적으로 학습에 방해가 되었다고 해석했습니다.)

그래서 이를 해결하고자 transformer block 별로 graident scaling을 수행하였습니다. Mixed precision training과 비교하면, 모델 전체에 적용되던 scaling을 각 block별로 적용하였다는 점에 있으며, grad scale(=scaling factoer)은 다음과 같이 변화합니다.

• 초기값 : $2^{13}$ * M (M is the number of GPUS)
• 매 update마다 $2^{1/1000}$ (약 1.0007)을 곱해줌
• 만약 nonfinite value가 발생하면, $\sqrt2$를 나눠주고 update를 스킵
• 모든 grad scale은 [$2^{7}$ * M, $2^{24}$ * M] 구간으로 clamp

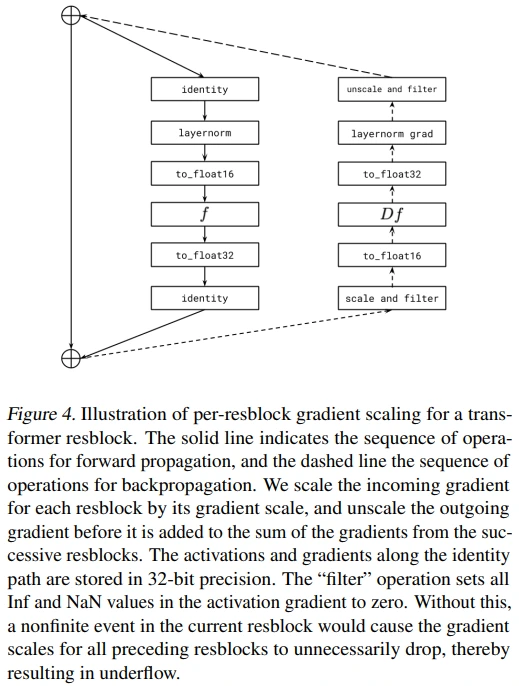
전체적인 모습은 figure 4에서 확인할 수 있습니다. Forward pass는 좌측, backward pass는 우측입니다. 눈여겨볼 부분은 backward 처음의 scale and filter, 마지막의 unscale and filter 입니다. (filter는 Inf나 NaN 같이 backprop 할 수 없는 gradient를 0으로 만드는 과정입니다.) 참고로 TPU + bfloat16 조합에서는 underflow 현상이 없었다고 하네요!

이외에도 Appendix D. Guidelines for Mixed-Precision Training의 내용을 추가로 설명하겠습니다.

• Only use 16-bit precision where it is really necessary for performance

  • DALL-E 학습에 적용되는 gradient compression 기법인 PowerSGD가 matrix의 rank 분해를 기반으로 하기 때문에, 1D parameter(gain, bias, embedding, unembedding)는 32-bit precision, 32-bit gradient, 32-bit Adam moments를 사용했다고 합니다.

  • Image token, text token의 경우에는 32-bit precision을 적용하였습니다. (gradient, Adam moment 언급은 없어서 16-bit를 사용했으려나 싶네요.) (참고: encoder, decoder)

• Avoid underflow when dividing the gradient

  • Data-parallel 학습을 하면, 필연적으로 gradients를 전체 worker 수 M만큼 나눠줘야 합니다. 그런데 16-bit precision gradient는 수 표현 범위가 제한되기 때문에 underflow, overflow 현상이 나타날 수 있습니다.

    • 먼저 나눈 다음, all-reduce로 더하면, 나누는 과정에서 underflow 현상에 취약해지고,
    • 먼저 all-reduce로 더한 다음, 나누면, 더하는 과정에서 overflow 현상에 취약해지게 됩니다.

  • 저자들은 전자의 flow를 base로 하며, all-reduce operation 이전에, per-parameter gradient의 scalar hitogram을 통해 underflow와 overflow가 발생하지 않도록 하는 값을 나눠주는 방식을 선택했다고 합니다. (그냥 단순히 custom하게 정했다고 생각하셔도 좋을 것 같습니다.)

2.5. Distributed Optimization

background: Recompute attention weights

Recompute 내용을 이해하려면 Sparse Transformer의 5.4. Saving memory by recomputing attention weights에 대한 이해가 필요합니다.

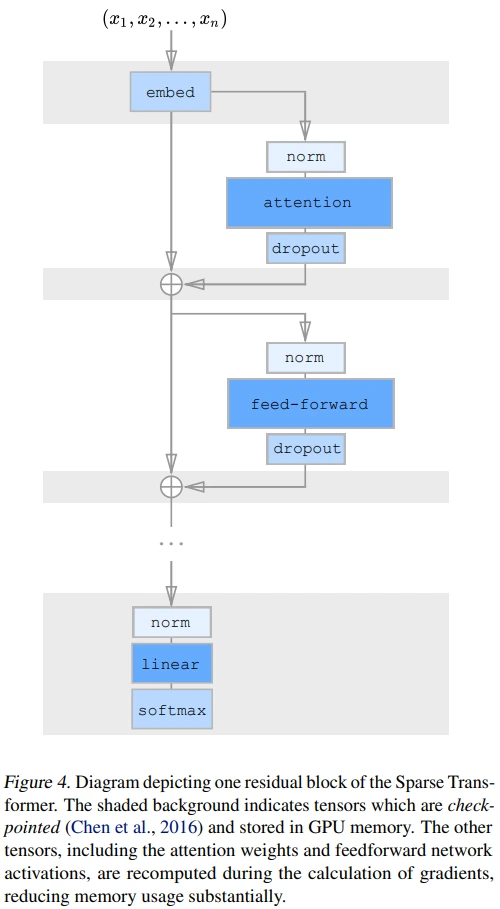
간단히 요약하면, 메모리 복잡도가 제곱인 self-attention이나 hidden dim을 4배 키우고 줄이는 feed-forward network처럼 연산 결과 저장에 많은 메모리가 필요한 경우, 중간 결과만 저장하여 해당 연산을 recompute하는 것이 경제적이라는 내용입니다. (gradient checkpointing 기법과 비슷합니다.) 이는 figure 4에서 어두운 음영 처리된 영역의 gradinet만 저장된다고 생각하시면 되고, 구현의 용이성을 위해 attention block의 dropout은 제거했다고 하네요.

background: PowerSGD

PowerSGD는 low-rank 분해를 기반으로 gradient compression을 수행하는 optimizer wrapper의 느낌으로, SAM optimizer와 비슷하다고 생각하셔도 될 것 같습니다.

참고로, DALL-E 논문의 error buffer 개념은 PowerSGD의 error feedback을 차용한 것으로 추측됩니다. Error feedback은 low-rank 분해를 기반으로 optimize하기 때문에 어쩔 수 없이 생기는 오차를 의미하며, 매 update 과정에 error가 feedback된다 정도로 이해하시면 될 것 같습니다.

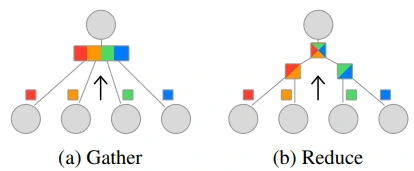
또한, PowerSGD 논문에서 Efficient aggregation between workers에서는 linearity 성질에 대한 내용이 있습니다. 이러한 특성 덕분에 all-reduce operation의 효율성을 높일 수 있었는데요. 간단히 말해서 PowerSGD에서 gather의 경우 linear 시간복잡도를 갖는데 반해 reduce는 log 시간복잡도를 갖기 때문에, 통신 비용이 큰 all-reduce를 효과적으로 수행할 수 있습니다.

Distributed Optimization

저자들은 메모리 사용량을 줄이기 위해 [ZeRO] 논문의 parameter sharding을 적용했습니다. (읽어보지 않았지만, ZeRO 논문에서 parameter partitioning을 의미하는 것으로 추측됩니다.) 특히, node(=machine) 내 통신보다 node 간 통신의 cost가 비싼 편인데 (all-reduce가 비쌈), low-rank를 기반으로 하는 PowerSGD로 gradient를 압축하여 이를 해결하려 했습니다.

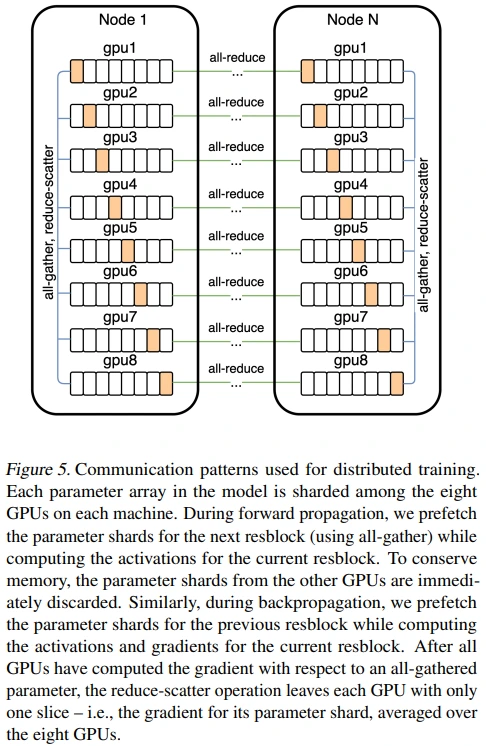
자세한 내용은 figure 5에서 확인해볼 수 있는데요.

• 현재 block에 대한 activation을 계산하는데 (backward의 경우 gradient도 계산), 이 과정에서 reduce-scatter operation으로 node 내 GPU들의 gradients 평균을 얻고, 그중 각 GPU에 해당하는 parameter shard만 남깁니다.
• 다음 resblock의 parameter sharding prefetch를 하는데, 이 과정에서 all-gather operation을 수행합니다.

이제 gradients 계산 과정에 PowerSGD의 low-rank 개념을 추가할 것입니다. (각 GPU에 해당되는 parameter shard gradients로 계산된 low-rank factor로부터 얻은) decompressed gradients와 (reduce-scatter로부터 얻은) node 내 gpu들의 gradients 평균 사이의 잔차를 error buffer로 설정하면 됩니다.

마지막으로, 각 GPU에 남게 되는 parameter shard gradient를 기반으로 low-rank 분해를 하여 (W=PQ), P와 Q 각각에 대해서 all-reduce operation을 수행하게 됩니다. (참고: Appendix E.2. Implementation Details)

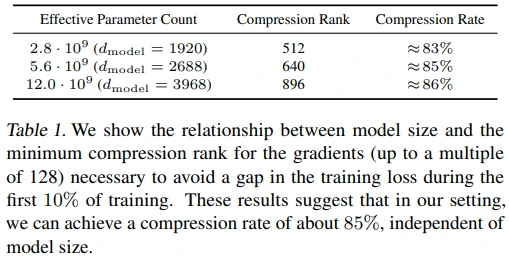
이렇게 PowerSGD의 low-rank 분해를 사용할 경우, 모델 크기에 상관없이 약 85% 정도의 gradient 압축이 가능하다고 합니다. (Compress rank 값을 설정할 때, 학습 초기 10% 구간의 loss gap을 중요하게 고려했다고 하네요. PQ 분해와 관련해서는 Appendix E.1. Bandwidth Analysis을 참고해주세요.)

또한, PowerSGD를 사용하며 저자들이 신경썼던 내용은 다음과 같습니다.

• Backprop. 과정에서 새로운 buffer를 사용하지 않고 error buffer에 gradient를 누적시켜 사용되는 메모리를 최적화했습니다. (아마도 PowerSGD의 linearity 특성 덕분에 가능했지 않나 추측됩니다.)
• (성능 하락을 유발하는) error buffer를 0으로 초기화하는 상황을 최소화했습니다. (Ex. mixed precision training에서의 nonfinite value, checkpoint로부터 학습을 이어서 할 경우)
• Numerical 안정성을 위해 Gram-Schmidt 대신 Householder orthogonalization을 사용했습니다. 둘 다 선형대수학의 QR decomposition이라는 행렬분해 기법입니다.
• Underflow를 피하기 위해 custom 16-bit format을 사용했다고 하며, 그 대상은 다음과 같습니다. (error buffers, their low-rank factors, all-reduce communication operations)

분산학습 관련 내용들은 Appendix E.2. Implementation Details에 자세하게 서술되어 있으니, 더 궁금하신 분은 찾아보셔도 좋을 것 같습니다.

2.6. Sample Generation

Caption과 생성된 이미지 사이의 CLIP score를 기반으로 output quality를 reranking 할 수 있음을 보여주고 있습니다.

3. Experiments

3.1. Quantitative Results

Figure 3을 통해 이전의 모델들과의 성능을 비교하고 있는데, DALL-E의 outuput은 512개 중 CLIP score가 가장 높은 결과라는 점도 생각해야 합니다. 다른 모델에도 동일한 process가 적용된 결과도 보여주었으면 좋았을 것 같습니다.

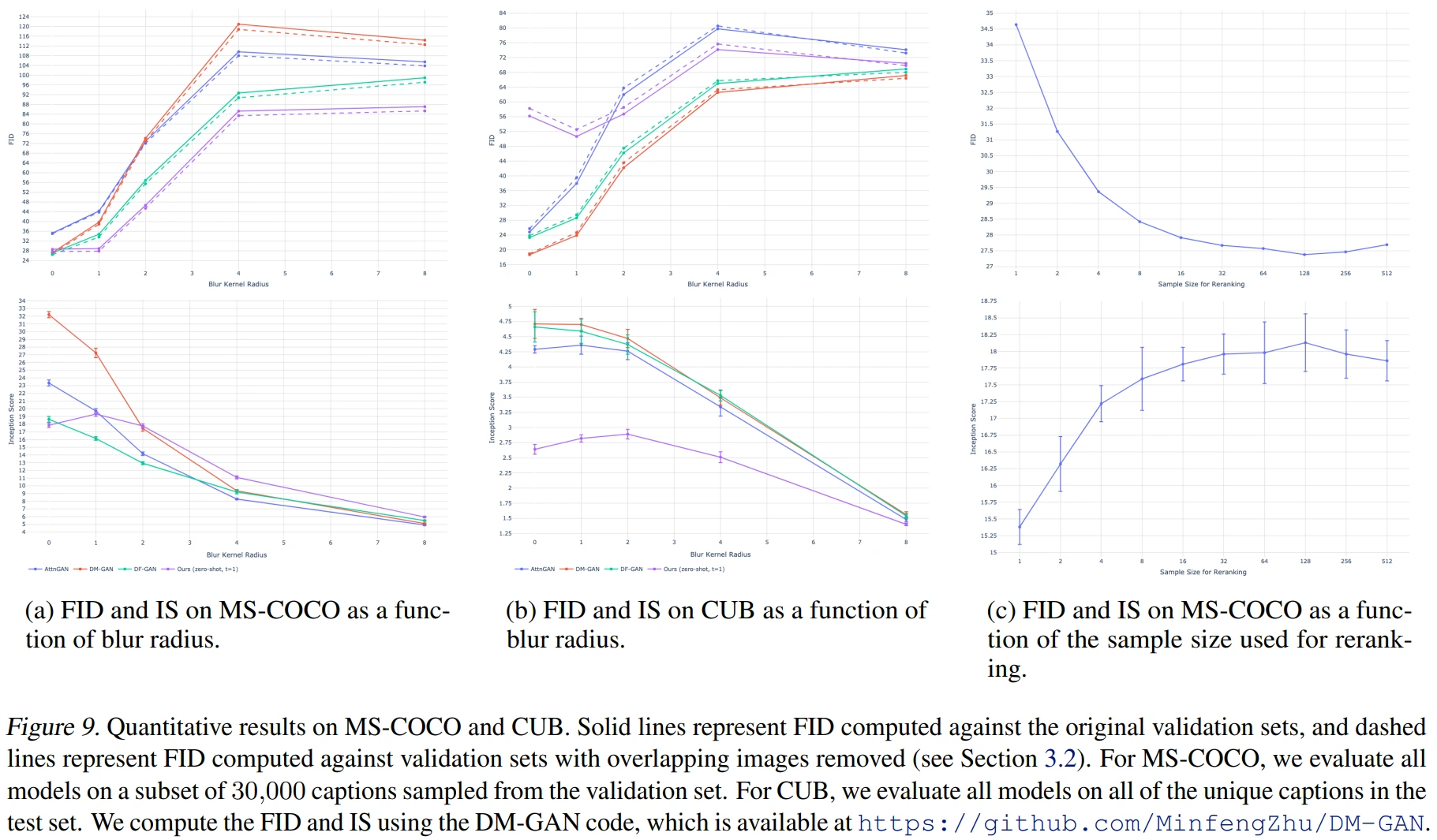
Figure 9는 (a) MS-COCO, (b) CUB, (c) reranking size 별 성능입니다. (FID는 낮을수록, IS는 높을수록 Good)

• (a) on MS-COCO, (b) on CUB

  • DALL-E train 이미지에 eval 이미지가 불가피하게 포함되었지만 (MS-COCO 21%, CUB 12%), 해당 dataset의 caption을 사용하지 않았고, 실선(중복 제거 X)과 점선(중복 제거 O)에 유의미한 성능 차이가 없었다는 점에서 cheat 성능이 아님을 주장합니다.

  • (a) MS-COCO dataset은 다른 모델들과 비교하여 좋은 성능을 보인다고 할 수 있지만, (b) CUB dataset에서는 zero-shot임을 고려하더라도 유독 좋지 않은 성능을 보이고 있습니다. (CUB dataset 성능 개선 방향으로는 finetuning을 future work로 제안하고 있습니다.)

  • 또한, x축은 blur kernel radius 입니다. 갑자기 blur가 등장한 배경에는 DALL-E가 pixel이 아닌 token을 처리함으로써, high frequency detail 보다는 low frequency information에 집중하기 때문입니다. 즉, DALL-E는 애초에 high frequency detail을 학습하지 않았기 때문에, 생성된 이미지에 blur 처리를 하여 low frequency information 측면에서 다른 모델과 성능을 비교해보자는 아이디어라고 할 수 있습니다. 결과적으로 더 강한 blur가 적용될수록 다른 모델보다 DALL-E의 성능이 상대적으로 좋아지는 경향을 확인할 수 있습니다.

• (c) : Reranking size는 32까지 성능과 비례하는 모습을 보이며, 128 이상인 경우에는 오히려 성능이 하락하는 측면도 확인해볼 수 있습니다.

3.2. Data Overlap Analysis

CLIP의 중복 제거 방식을 사용했습니다. 중복 제거를 위한 contrastive model을 사용하여 closeness score를 계산하였고, false negative rate를 낮추는 방향으로 threshold를 직접 정했다고 합니다.

3.3. Qualitative Findings

• (a) : 실존하지 않는 추상적인 개념에 대한 생성이 가능한 것으로 보입니다.
• (b) : 개념들 간의 관계도 이미지 상에 나타낼 수 있는 것으로 보입니다. (일관적인 성능을 보장하지는 않는다고 언급합니다.)
• (c) : 글자가 반영된 이미지 또한 생성됩니다. (반복적인 text prompt로 만든 것도 확인해볼 수 있습니다.)
• (d) : 입력된 text를 기반으로 Image-to-Image translation도 가능합니다.

Reference

• lucidrains’ DALLE-pytorch

• Gumbel-Softmax 리뷰

• Why is Laplace prior producing sparse solutions?

• Mixed-Precision-Training