[논문리뷰] SimSiam: Exploring Simple Siamese Representation Learning (CVPR ‘21 Best Paper Honorable Mentions)
Abstract
Image에 augmentation을 적용하고 siamese network로 학습하는 self-supervised learning 방식에서 stop-gradient operation이 (negative sample, large batch, momentum encoder 보다) collapsing을 방지하는 중요한 역할을 한다.
1. Introduction
Collapsing이란, similarity를 높이는 방식으로 학습하다보니 각 image에서 good representation을 추출하지 못하고 constant output을 내뱉는 현상을 의미합니다. (어떤 input에 대해서도 동일한 output을 내뱉게 된다면 similarity를 높아지기 때문)
그래서 collapsing을 방지하기 위한 여러 솔루션들이 적용되어 왔습니다. SimCLR에서는 negative pair를 추가한 contrastive learning을, SwAV에서는 online clustering을, BYOL에서는 momentum encoder를 사용하며 collapsing을 방지할 수 있었습니다.
SimSiam의 저자들은 이러한 솔루션들이 핵심이 아니며 stop-gradient가 중요한 역할을 한다고 주장합니다. 그리고 optimization 관점의 가설로 이를 증명하였습니다. (개인적으로 two augmented image + siamese network 학습 방식이 invariance feature를 추출하는 inductive bias를 가진다는 관점이 흥미로웠습니다.)
3. Method
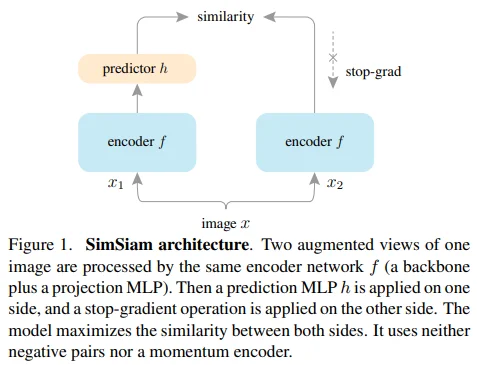

Figure 1과 pseudo-code를 통해 SimSiam의 전체적인 구조를 확인할 수 있습니다. 이름 그대로 간단합니다.
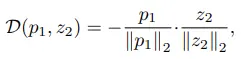
Objective로는 (BYOL의 l2 normed MSE loss와 동일하게) negative cosine similarity를 사용하였으며, symmetrized loss 형태입니다.
4. Empirical Study
요약 : stop-gradient를 적용하지 않거나 predictor MLP를 제거하는 경우에만 collapsing 현상이 나타난다. (batch size, batch normalization, similarity function, symmetric loss는 collapsing을 방지하는 주요 factor가 아니다.)
4.1. Stop-gradient
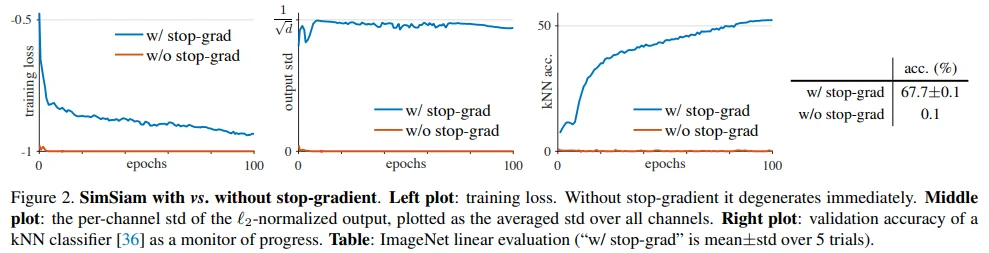
SimSiam 모델에서 stop-gradient 유무에 따른 성능을 비교하였습니다.
- w/o stop-grad train loss가 -1에 수렴 (= collapsing)
- w/ stop-grad output std가 $1/\sqrt{d}$에 수렴
- output vector z ~ i.i.d $N(0,1)$인 경우, std가 $1/\sqrt{d}$에 근사된다고 하네요.

4.2. Predictor

- (a) : predictor가 없는 경우, collapsing
- (b) : predictor를 random weight로 고정한 경우, loss가 수렴하지 않음
- (c) : predictor의 lr을 decay하지 않는 경우, 더 높은 acc (+ 0.4% acc)
- 저자들은 predictor가 latest representation을 반영할 수 있어야 하기 때문에, 굳이 lr decay할 필요가 없을 것으로 추측
4.3. Batch Size
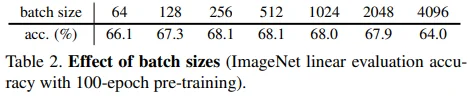
256부터 2048에 이르기까지 batch size와 무관한 성능을 보이고 있으며, 64와 128의 경우에는 약간의 성능 저하를 확인할 수 있습니다. 높은 batch size(4096)에서의 성능 저하는 SGD optimizer에서 기인한 것으로 볼 수 있습니다.
4.4. Batch Normalization

- (a) : acc가 낮긴 하지만 collapsing을 보이지는 않는다. (optimization에 어려움을 겪는 것으로 추정)
- (b) : hidden BN 추가
- (c) : projection MLP에 output BN 추가 (추가로, output BN의 affine transform을 제거하면, + 0.1% acc)
- (d) : prediction MLP에 output BN 추가 (collapsing은 아니지만, 학습이 불안정함)
요약하면 BN을 적절한 위치에 사용하면 학습에 도움이 되지만, collapsing과는 무관하다고 주장합니다.
4.5. Similarity Function
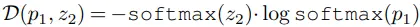
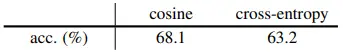
Cosine similarity를 cross-entropy similarity로 대체하였을 때에도 collapsing 없이 준수한 성능을 보였습니다. 이를 통해 cosine similarity가 collapsing 방지에 중요한 요소가 아니라고 주장합니다. (softmax는 채널 축을 따라서 d차원에 대해 동작)
4.6. Symmetrization

Asymmetric loss에서도 collapsing 현상은 발견되지 않았고, loss update양을 보정하기 위해 2배를 해주자 symmetric loss와 비슷한 성능을 보였습니다.
5. Hypothesis
요약 : SimSiam은 alternating optimization으로 설명할 수 있으며, 이러한 가정에 따라 stop-gradient operation의 필요성을 확인할 수 있다. 또한, predictor MLP는 augmentation 분포에 대한 근사를 돕는 역할을 하는 것으로 보이며, $\eta$에 대한 moving average 실험을 근거로 momentum encoder가 이러한 역할을 일부 수행하는 것으로 보인다.
5.1. Formulation
저자들은 2개의 변수와 2개의 sub-problem으로 구성된 Expectation-Maximization (EM) 알고리즘으로 SimSiam을 설명할 수 있다고 가정합니다. 이를 위해, SimSiam의 objective를 수식으로 재정의하면 다음과 같습니다. (편의를 위해 현재 상황에서 predictor는 고려하지 않으며, 추후 다룰 예정입니다.)
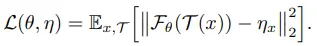
- $\theta$ : encoder network $\mathcal{F}$의 parameter
- $\eta$ : stop-gradient를 설명하기 위한 변수
- $\theta$처럼 network의 parameter 형태로 표현할 필요가 없기 때문에 $\eta$로 간소화하여 표현
- $\eta_{x}$ : representation of image x
- $\mathcal{T}$ : augmentation
전체적으로 image x와 augmentation $\mathcal{T}$ 분포에 대한 expectation이 걸려있으며, 그 안에 encoder network $\mathcal{F}$와 $\eta$에 대한 (l2 normed) MSE loss가 존재하는 형태입니다.
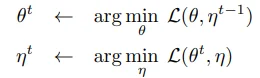
저자들이 EM 알고리즘을 언급한 이유는 위 2개의 sub-problem 수식에서 확인할 수 있습니다. 이는 $\theta$와 $\eta$ 각 변수를 순차적으로 optimize하면 objective의 해를 찾을 수 있다는 관점인데요.
더 나아가, 이러한 alternating algorithm의 형태는 마치 k-means clustering과 유사한 면이 있다고 언급합니다. (추가로, 2개의 augmented view 사이의 similarity를 높이는 과정이 clustering과 유사하다고 생각할 수도 있을 것 같습니다.)
- $\theta$ = clustering center
- $\eta$ = assignment vector of image x
One-step alternation
지금까지 SimSiam이 EM 알고리즘, k-means clustering과 유사하다는 저자들의 가정을 살펴보았고, 위 가정이 SimSiam에 적합하다는 점을 이론적으로 살펴보겠습니다.
먼저, $\eta$를 각 image x에 대한 변수인 $\eta_x$로 표현하면 아래 수식들을 얻을 수 있습니다.
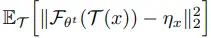
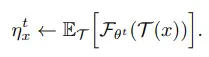
그리고 augmentation $\mathcal{T}$는 학습 과정에서 sampling되기 때문에 $\mathcal{T}^{\prime}$으로 근사시킬 수 있으며, 이 과정에서 expectation을 무시할 수 있게 됩니다. (augmentation 분포를 알지 못하기에 수식 전개를 위한 선택)
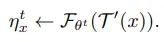
마지막으로 위 수식을 $\theta$에 대한 update 식에 대입하면 아래 수식이 됩니다.
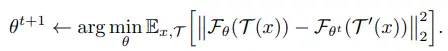
결과적으로 $\eta$는 식에서 사라졌고, $\theta^{t+1}$를 얻기 위해서는 $\theta^t$가 필요하다는 사실을 수식으로 확인할 수 있습니다. (여기서 $\theta^t$와 관련 있는 부분이 stop-gradient operation을 의미하게 됩니다.)
Predictor
이제 predictor h를 고려할 차례입니다. 앞선 수식 전개 과정에서 sampling을 활용하여 augmentation $\mathcal{T}$에 대한 expectation을 무시했는데요.
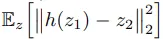
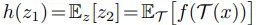
바로 위 식과 SimSiam의 구조를 생각해보시면, predictor h와 $\mathbb{E}_{\mathcal{T}}$이 같은 위치에 존재하는 것을 볼 수 있습니다. 즉, 학습을 통해 predictor가 augmentation $\mathcal{T}$ 분포를 근사할 수 있고, 단순히 sampling으로 근사하는 것보다 더 tight해질 수 있다고 주장합니다. (어디까지나 이론적인 입장)
Symmetrization
마지막으로 symmetric loss를 고려할 차례입니다. 저자들은 symmetrization이 augmentation $\mathcal{T}$에 대한 dense sampling으로 해석할 수 있다고 주장합니다. 즉, $\mathcal{T}_1$-$\mathcal{T}_2$ pair와 함께, $\mathcal{T}_2$-$\mathcal{T}_1$ pair도 고려할 수 있게 된다는 내용입니다. (augmentation에 대한 근사를 더 잘할 수 있다는 해석도 가능할 것 같습니다.)
5.2. Proof of concept
Multi-step alternation
저자들은 k SGD step마다 $\theta$를 update하는 실험을 진행합니다. 참고로, $\eta_x$는 매 update마다 필요한 만큼 미리 계산하여 memory에 cache하였다고 하네요.

위 표를 통해 step이 많아지더라도 collapsing이 발생하지 않는 것을 확인할 수 있습니다. (1-step = SimSiam) SGD optimizer를 사용했기에 가능한 현상 같기도 합니다.
Expectation over augmentations
Expectation over augmentation을 근사(무시)하는 대신에, $\eta_x$에 moving average를 적용해보는 실험을 합니다. (momentum encoder와 유사)
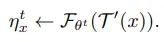
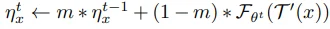
위 식을 아래 식으로 대체하고 predictor h를 제거하였더니, 55% accuracy를 보였습니다. (momentum coefficient는 0.8을 사용했는데, momentum encoder에서는 보통 0.99 정도의 높은 값을 사용하기 때문에 이에 대한 ablation이 있었으면 좋았을 것 같네요.)
5.3. Discussion
지금까지의 가설과 실험은 SimSiam의 optimization이 이루어지는 방식에 대한 것일뿐, 어떻게 collapsing을 방지할 수 있는지에 대해서는 다루지 못했습니다.
이에 대한 저자들의 생각은 다음과 같습니다. 비록 학습 초기에는 $\eta$가 random init network로부터 얻어지므로 constant에 해당하지만, alternating optimizer가 global x에 대한 gradient를 계산하는 것이 아니라, 파편화된 $\eta_x$에 대한 gradient를 계산하기 때문에, collapsing 현상이 발생하기 어려웠을 것이라고 추측합니다.
6. Comparisons
6.1. Result Comparisons
ImageNet

ImageNet linear evaluation 성능입니다. (ResNet50, two 224x224 views, single crop)
100 epoch에서는 좋은 성능을 보이지만, 200, 400, 800 epoch에서는 BYOL에 비해 꽤 낮은 성능을 보이고 있네요. 그럼에도 momentum encoder와 large batch size가 필요하지 않다는 점에서 memory-efficient한 학습 방식이라고 생각됩니다. (memory 관련 figure가 있었다면 더 좋지 않았을까 싶네요.)
Transfer Learning
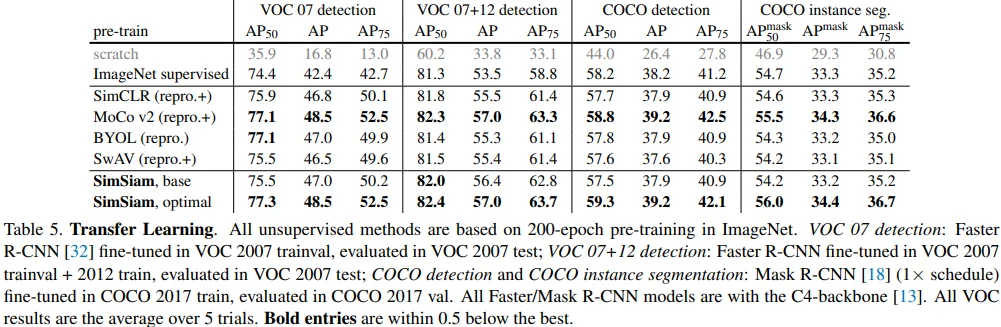
ImageNet 성능에 비해 SimSiam의 transfer learning 성능은 준수한 것으로 보입니다. 특이한 점은 learning_rate와 weight_decay parameter를 수정하였더니, ImageNet classification 성능에는 별 차이가 없었지만 transfer learning 성능은 크게 상승하였다고 합니다. (base -> optimal)
6.2. Methodology Comparisons
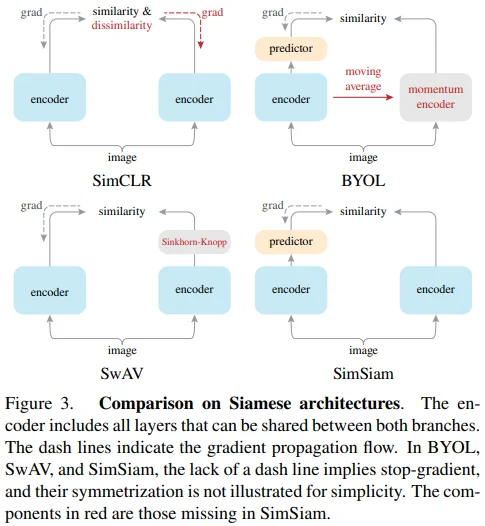
SimSiam의 가장 유명한 figure로, SimSiam에 존재하지 않는 개념은 빨간 글씨로 강조되었습니다.
Relation to SimCLR : SimCLR without negatives

SimCLR에 predictor와 stop-gradient를 추가해보았지만, 성능은 오히려 하락하였습니다. 이에 대해 저자들은 SimCLR의 contrastive learning이 SimSiam의 alternating optimization 방식과는 상이하기 때문이라고 추측하고 있습니다.
Relation to SwAV : SwAV without online clustering
SwAV를 SimSiam의 형태로 표현하기 위해 다음의 간소화 과정이 필요합니다.
- Shared prototype layer는 siamese encoder에 포함되는 것으로 간주합니다.
- SwAV의 prototype은 gradient가 끊긴 채로 weight normalization 되는데, reproduce 과정에 Weight Normalization 논문을 적용하여 end-to-end로 gradient가 흐르게 하면서, original SwAV와 비슷한 결과를 얻었다고 합니다.
- SwAV에서는 similarity 함수로 cross-entropy를 사용합니다.
또한, SwAV에는 Sinkhorn-Knopp (SK) transform을 통해 online clustering을 수행하는데, 균형 있게 clustering될 수 있도록 하는 제약사항이 존재합니다. 즉, 이러한 제약사항이 SwAV의 collapsing을 방지할 수 있도록 기여하지만, 안타깝게도 SimSiam에는 이러한 매커니즘을 설명할 수 있는 개념이 존재하지 않습니다. (쉽게 말하면 SK transform은 SimSiam의 format으로 설명할 수 없다는 내용입니다.)

SwAV에 대해서는 2개의 ablation을 진행합니다.
- w/ predictor : 성능 소폭 하락
- remove stop-gradient : divergence
- 이에 대해 저자들은 clustering based method인 SwAV도 alternating 형태로 학습하기 때문에, stop-gradient가 중요한 역할을 하고 있을 수도 있다고 추측합니다.
Relation to BYOL : BYOL without momentum encoder
저자들은 $\eta$ sub-problem을 해결하는 과정에서 predictor가 $\mathbb{E}_{\mathcal{T}}$를 근사하는 역할을 한다고 추정하였습니다. 그리고 5.2. Expectation over augmentations에서 $\eta$에 대한 moving average가 predictor의 역할을 일부 수행하는 것으로 보이는 결과도 얻었습니다.
이를 종합하여 $\eta$ sub-problem이 gradient-based optimization에 의해 해결될 수 있지 않을까, 그리고 이러한 optimization을 momentum encoder와 연결지을 수 있지 않을까 하는 futurew work를 제안하고 있습니다.